ADDITION OF VECTORS

METHOD OF ADDITION OF TWO VECTORS

• When two vectors are in the same direction
• When two vectors are in the opposite direction
• When two vectors are perpendicular to each other

ADDITION OF VECTORS

• By head to tail rule
• Analytical determination of the resultant of two vectors using parallelogram law
• The general method of adding two vectors using triangle law

Methode of Addition of Two Vectors

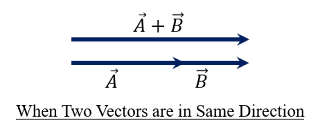
When two vectors are in the same direction

When two vectors `\vecA` and `\vecB` are in the same direction, then the magnitude of the resultant vector can be obtained by simply adding the magnitudes of the individual vectors i.e.

`\Rightarrow`                      |`\vecA+\vecB`| `=|\vecA|+|\vecB|`

The direction of the resultant vector is the same as that of the vector `\vecA` and `\vecB` 

When two vectors are in the opposite direction

When two vectors `\vecA` and `\vecB` are in the opposite direction and the vector `\vecA` has greater magnitude then the magnitude of the resultant vector is equal to the difference of the magnitudes of the vector `\vecA` and `\vecB` i.e.

`\Rightarrow`                      |`\vecA-\vecB`| `=|\vecA|-|\vecB|`

The direction of the resultant vector is in the direction of the vector `\vecA` which has greater magnitude.

When two vectors are perpendicular to each other

When two vectors are perpendicular to each other (say vector `\vecA` and `\vecB`) then the magnitude of the resultant vector is obtained by Pythagoras's theorem i.e.

`\Rightarrow`                      |`\vecA+\vecB`| `=\sqrt{|vecA|^2+|vecB|^2}`

The direction of the resultant vector can be determined by trigonometric functions say vector `\vecA` as the base and vector `\vecB` as perpendicular then: 

`\Rightarrow`                      `\theta=\tan^{-1}\left(\frac BA\right)` 

ADDITION OF VECTORS

By Head to Tail Rule

• Vectors are always added graphically according to the head to tail rule. The following steps should be carried out to add two or more than two vectors.
• Choose a particular coordinate system.
• Select a suitable scale according to the magnitudes of the physical quantities.
• Draw the first vector by using this scale.
• Draw the second vector using the scale plotting the tail (initial point of the second vector on the head (terminal point) of the first vector.
• The head (terminal point) of the second vector is joined with the tail (initial point) of the third vector.
• Similarly, draw all the given vectors one by one.
• Now the straight-line directed from the tail (initial point) of the first vector to the head (terminal point) of the last vector represents the resultant vector.
• Now, measure the line and reconvert it into its real magnitude with the help of the chosen scale.

General Method of Adding Two Vectors Using Triangle Law

If the vectors `\vecA` and `\vecB` are joined by "Head to Tail Rule" to form the sides of a triangle as shown in the figure then the resultant vector is given by:

`\Rightarrow`                      `\vecR=\vecA+\vecB`

If two vectors `\vecA` and `\vecB` form an angle "`\theta`" with each other then the magnitude of the resultant vector may be determined by:

`\Rightarrow`                      |`\vecR`| `=\sqrt{|vecA|^2+|vecB|^2+2ABCos\theta}`

It must be remembered that "`\theta`" is the angle between the vector `\vecA` and `\vecB`.

`\Rightarrow`                      `\phi=\cos\theta\left(\frac{A^2+R^2-B^2}{2AR}\right)=\tan^{-1}\left(\frac{B\sin\theta}{A+B\cos\theta}\right)`

Analytical Determination of the Resultant of Two Vectors Using Parallelogram Law

If the vectors `\vecA` and `\vecB` are joined by "Head to Tail Rule" to form a parallelogram as shown in the figure then the magnitude of the resultant vector is given by:

`\Rightarrow`                      `|vecR|=|vecA+vecB|= sqrt{A^2+B^2-2ABCos\left(180-\theta\right)}`

`\Rightarrow`                      `|vecR|=|vecA+vecB|= sqrt{A^2+B^2+2ABCos\theta}`

where `\theta` is the angle between the vectors `\vecA` and `\vecB`. The above formula is developed from the "Law of Cosines".

For Subtraction:

`\Rightarrow`                      `|vecR|=|vecA-vecB|= sqrt{A^2+B^2-2ABCos\theta}`

For Direction:

The direction of the resultant vector may be given by the angle `\alpha` and `\beta` as shown in the diagram. The angles `\alpha` or `\beta` can be determined by:

`\Rightarrow`                      `\frac{Sine\alpha}B=\frac{Sine\beta}A=\frac{Sin\theta}R`

Or

`\Rightarrow`                      `\frac{Sin\alpha}|vecB|=\frac{Sin\beta}|vecA|=\frac{Sin\theta}|vecR|`

This is called the "Law of Sines"